CLASE DE GEOMETRIA GRADO 11° DEL 11 DE ABRIL DEL 2024 SEMANA #8 TEMA ECUACION DE LA CIRCUNFERENCIA EJERCICIOS

   

	ÁREA: GEOMETRIA	GRADO: 11°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL 11 DE ABRIL DEL 2024	PERIODO: PRIMERO
	VALOR: RESPETO	FRASE:  “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION”

FECHA: DEL 11 DE ABRIL DEL 2024

 GRADO: 11°

TEMA: ECUACION DE LA CIRCUNFERENCIA EJERCICIOS

SUBTEMA: ECUACION DE LA CIRCUNFERENCIA EJERCICIOS

LOGRO. Reconoce la geometría analítica en el desarrollo para su formación de figuras planas

ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿Porque ecuación?. lluvia de ideas.

ECUACION DE LA CIRCUNFERENCIA. EJERCICIOS

Ejercicio 1

Halla la ecuación de la circunferencia que tiene de centro el punto C(-2,3) y de radio r=4. ¿Pertenecen los puntos A(2,3), B(-4,3) y D(1,5) a la circunferencia?

En este caso tenemos el centro y el radio:

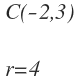
Por tanto, en la siguiente expresión:

Sustituimos las coordenadas del centro y el radio por sus valores:

Desarrollamos los productos notables y el cuadrado del segundo miembro:

Y reordenamos términos para obtener la ecuación de la circunferencia en su forma general:

Para saber si cada uno de los puntos pertenecen a la circunferencia, debemos sustituir las coordenadas de cada punto por x y por «y» y comprobar si se cumple la igualdad. Si se cumple, el punto pertenece a la circunferencia y en caso contrario, el punto no pertenece.

Para ver si el punto A(2,3) pertenece a la circunferencia, sustituimos x por 2 e «y» por 3:

Operamos en el primer miembro y vemos que efectivamente el resultado es 0, igual al del segundo miembro, por tanto el punto A sí pertenece a la circunferencia:

Comprobamos ahora el punto B(-4,3), sustituyendo x e «y» por las coordenadas del punto:

Al operar en el primer miembro, el resultado no es igual al del segundo miembro, luego el punto B no pertenece a la circunferencia:

Por último, hacemos lo mismo con el punto C(1,5):

El resultado del primer miembro no es igual a cero, por lo que el punto C tampoco pertenece a la circunferencia:

Ejercicio 2

Hallar la ecuación de la circunferencia que pasa por el punto A(2,-1) y cuyo centro es C(-1,3).

En este ejercicio conocemos el centro y un punto de la circunferencia:

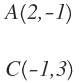
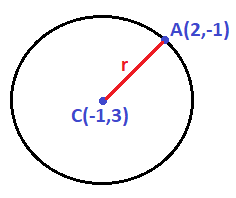
Nos falta conocer el radio de la circunferencia para poder calcular su ecuación, que es igual a la distancia entre el punto A y el centro C:

Ahora ya conocemos el centro y el radio:

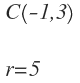
Por tanto, ya podemos calcular la ecuación de la circunferencia.

En la siguiente expresión:

Sustituimos a, b y r por sus valores:

Operamos:

Y reordenamos términos para dejar la ecuación en su forma general:

ACTIVIDAD EN CASA:

Determina la ecuación de la circunferencia que pasa por los siguientes tres puntos: