CLASE DE MATEMATICA GRADO 10° DEL 9 Y 11 DE ABRIL DEL 2024 SEMANA #8 TEMA: FUNCIONES TRIGONOMETRICAS DE ANGULOS GENERALES

	ÁREA: MATEMATICA	GRADO: 10°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL 9 Y 11 DE ABRIL DEL 2024	PERIODO: PRIMERO
	VALOR: RESPETO	FRASE:   “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION”

FECHA: DEL 9 Y 11 DE ABRIL DEL 2024

 GRADO: 10°

TEMA: FUNCIONES TRIGONOMETRICAS DE ANGULOS GENERALES

SUBTEMA: VALORES EXANTOS DE LAS FUNCIONES TRIGONOMETRICAS DE THETA DADO UN PUNTO EN EL LADO TERMINAL

LOGRO. Usa ángulos coterminales para encontrar el valor exacto de una función trigonométrica

ACTIVIDAD PREVIA: Exploro mis conocimientos. "localización de un avión en vuelo". lluvia de ideas.

FUNCIONES TRIGONOMETRICAS DE ANGULOS GENERALES

Ángulos coterminales

Los ángulos coterminales son ángulos en posición estándar (ángulos con el lado inicial en el eje positivo de las x ) que tienen un lado terminal común. Por ejemplo 30°, –330° y 390° son todos coterminales.

¿Qué son los ángulos coterminales?

Los ángulos coterminales son definidos como los ángulos que tienen el mismo lado inicial y el mismo lado terminal. Estos ángulos son considerados como equivalentes ya que indican la misma dirección. Es posible tener ángulos terminales positivos y negativos.

¿Cuál es la fórmula de los ángulos coterminales?

La fórmula para encontrar los ángulos terminales de un ángulo dado depende en si el ángulo dado está en radianes o en grados. Entonces, tenemos las siguientes dos fórmulas:

Grados: $�\pm 360^{\circ }�$ Radianes: $�\pm 2��$

en donde, n es cualquier número entero.

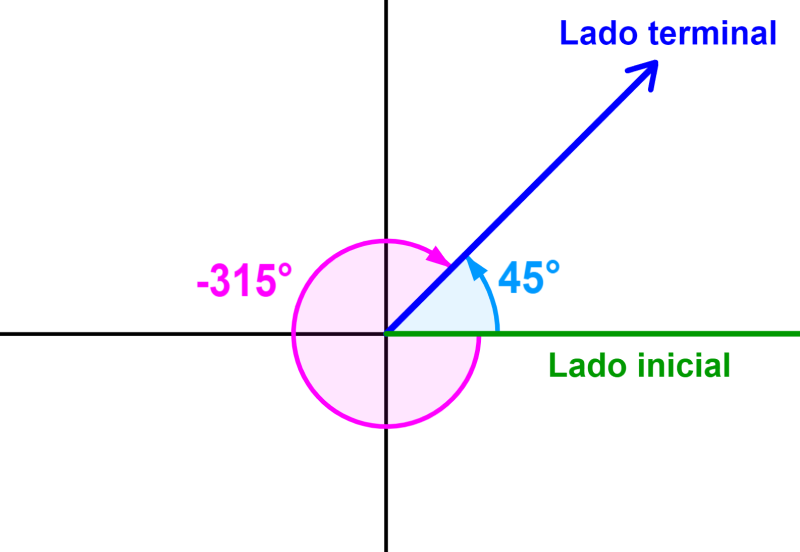
En el ejemplo de arriba, tenemos que 45° y -315° son coterminales. Podemos verificar esto al restarlos y observar que su diferencia es 360°:

$45^{\circ }-(-315^{\circ })=360^{\circ }$

También podemos encontrar otro ángulo coterm inal al ángulo de 45°:

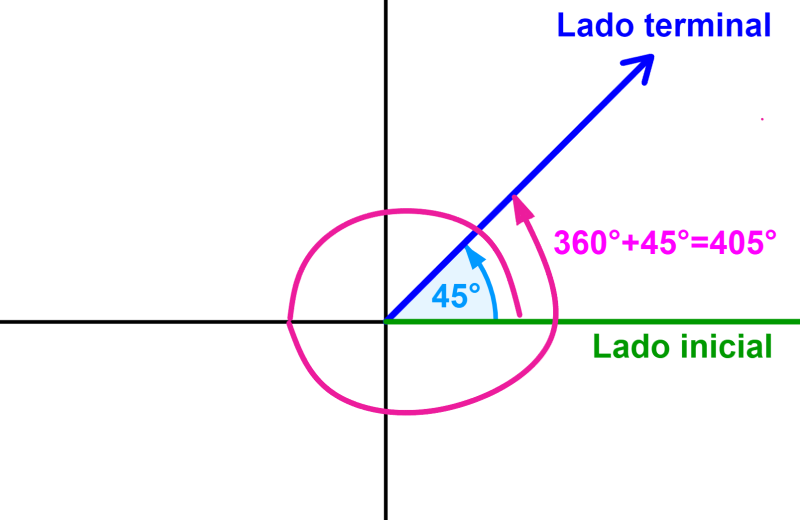
En este caso, observamos que la diferencia entre ambos ángulos es -360°, el cual es un múltiplo de 360°:

$45^{\circ }-405^{\circ }=-360^{\circ }$

Podemos concluir que dos ángulos son considerados coterminales si es que su diferencia es igual a un múltiplo de 360° o un múltiplo de 2π si es que el ángulo está en radianes.

De igual forma, podemos encontrar ángulos coterminales de un ángulo dado al sumar un múltiplo de 360° o un múltiplo de 2π al ángulo original.

Ángulos coterminales positivos o negativos

En el ejemplo de arriba, encontramos que 405° y -315° son los ángulos coterminales de 45°. Entonces, tenemos:

• 405° es el ángulo coterminal positivo de 45°
• -315° es el ángulo coterminal negativo de 45°

Entonces, podemos decidir si es que queremos sumar o restar múltiplos de 360° o de 2π dependiendo en si queremos obtener un ángulo coterminal positivo o negativo.

Ejercicios de ángulos coterminales resueltos

Las fórmulas de los ángulos coterminales son aplicadas para resolver los siguientes ejercicios. Cada ejercicio tiene su respectiva solución, en donde puedes mirar el proceso y razonamiento usados.

EJERCICIO 1

Encuentra dos ángulos coterminales de 30°.

solución

El ángulo dado es $�=30^{\circ }$. La fórmula para encontrar los ángulos coterminales es:

$�\pm 360�$

n puede ser cualquier número entero. Podemos usar $�=1$ y $�=-1$ para encontrar dos ángulos coterminales diferentes. Entonces, tenemos:

$�\pm 360�$

$=30^{\circ }+360(1)$

$=390^{\circ }$

Ahora, usando $�=-1$, tenemos:

$�\pm 360�$

$=30^{\circ }+360(-1)$

$=-330^{\circ }$

EJERCICIO 2

Encuentra dos ángulos coterminales de $\frac{�}{4}$.

solución

Tenemos el ángulo $�=\frac{�}{4}$. Este ángulo está en radianes, por lo que usamos la siguiente fórmula para encontrar los ángulos coterminales:

$�\pm 2��$

n puede ser cualquier número entero. En este caso, vamos a usar $�=2$ y $�=-1$. Entonces, tenemos:

$�\pm 2��$

$=\frac{�}{4}+2�(2)$

$=\frac{17�}{4}$

Ahora, usando $�=-1$, tenemos:

$�\pm 2��$

$=\frac{�}{4}+2�(-1)$

$=-\frac{7�}{4}$

    

Para encontrar un ángulo coterminal positivo y uno negativo con un ángulo dado, puede sumar y restar 360° si el ángulo es medido en grados o 2π si el ángulo es medido en radianes .

Ejemplo 1:

Encuentre un ángulo coterminal positivo y uno negativo con un ángulo de 55°.

55° – 360° = –305°

55° + 360° = 415°

Un ángulo de –305° y un ángulo de 415° son coterminales con un ángulo de 55°

Ejemplo 2:

Encuentre un ángulo coterminal positivo y uno negativo con un ángulo de  .

Un ángulo de  y un ángulo de  son coterminales con un ángulo de  .

ACTIVIDAD EN CASA:

EJERCICIO 1

Encuentra dos ángulos coterminales de 60°.

EJERCICIO 2

Encuentra dos ángulos coterminales de $\frac{�}{4}$.

2 REALIZA PAGINA 64 PUNTO 4