CLASE DE MATEMATICA GRADO 11° DEL 10 Y 12 DE ABRIL DEL 2024 SEMANA #8 TEMA: FUNCIONES POLINOMICAS

	ÁREA: MATEMATICA	GRADO: 11°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL 10 Y 12 ABRIL DEL 2024	PERIODO: PRIMERO
	VALOR: RESPETO	FRASE: “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION”

FECHA: DEL 10 Y 12 DE ABRIL DEL 2023

 GRADO: 11°

TEMA: FUNCIONES POLINOMICAS

SUBTEMA: FUNCIONES DE SEGUNDO GRADO

LOGRO. Reconoce el tipo de funciones a partir de su grafica

ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿Qué son funciones polinómicas?. lluvia de ideas.

FUNCION DE SEGUNDO GRADO O CUADRATICA

Función cuadrática (parábola)

Explicamos los conceptos básicos relacionados con las funciones cuadráticas y resolvemos algunos problemas.

Índice:

1. Definición y ejemplo
2. Vértice
3. Puntos de corte con los ejes
4. Formas factorizada y canónica

1. Definición y ejemplo

Una función cuadrática (o parabólica) es una función polinómica de segundo grado. Es decir, tiene la forma

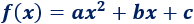
siendo $a\ne 0$.

Esta forma de escribir la función se denomina forma general.

La gráfica de una función cuadrática siempre es una parábola.

Ejemplo

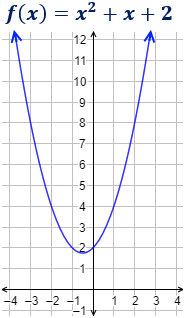
Las parábolas tienen forma de $\cup$ (si $a>0$) o de $\cap$ (si $a<0$).

Además de la orientación, el coeficiente $a$ es la causa de la amplitud de la función: cuanto mayor es $|a|$, más rápido crece (o decrece) la parábola, por lo que es más cerrada.

2. Vértice

Las funciones cuadráticas tienen un máximo (si $a<0$) o un mínimo (si $a>0$). Este punto es el vértice de la parábola.

La primera coordenada del vértice es

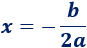
Y la segunda coordenada es su imagen:

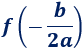
Ejemplo

Calculamos el vértice de la función

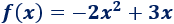
Identificamos los coeficientes:

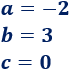
Como $a$ es negativo, la parábola tiene forma de $\cap$. El vértice es un máximo.

La primera coordenada del vértice es

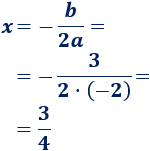
Calculamos la segunda coordenada:

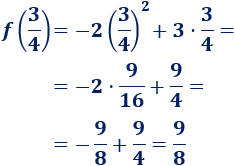
Por tanto, el vértice es el punto

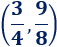
Gráfica:

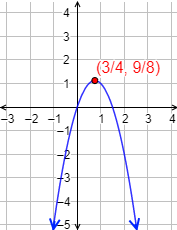
3. Puntos de corte con los ejes

Una parábola siempre corta el eje de ordenadas (eje Y) en un punto. Como esto ocurre cuando $x=0$, se trata del punto $(0,c)$ puesto que $f\left(0\right)=c$.

Una función corta al eje de abscisas cuando $y=0$. Por tanto, para hallar estos puntos de corte, tenemos que resolver una ecuación cuadrática:

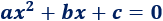
Como una ecuación cuadrática puede tener una, dos o ninguna solución, puede haber uno, dos o ningún punto de corte con el eje X.

Recordamos la fórmula que necesitamos:

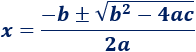
Ejemplo

Calculamos los puntos de corte de la función

Los coeficientes de la ecuación son $a=1$, $b=0$ y $c=-1$.

Eje Y:

El punto de corte con el eje Y es $(0,-1)$.

Eje X:

Resolvemos la ecuación de segundo grado:

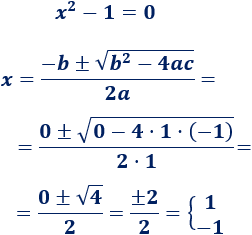
Hay dos soluciones: $x=1$ y $x=-1$.

La segunda coordenada es $0$.

Por tanto, tenemos los puntos de corte

Gráfica:

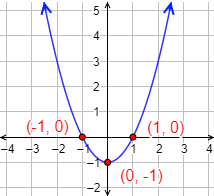
4. Formas factorizada y canónica

La forma factorizada de una función cuadrática es

donde $a$ es el coeficiente principal (visto anteriormente); $x_1$ y $x_2$ son las soluciones de la ecuación $a{x}^2+bx+c=0$.

• Si la ecuación $a{x}^2+bx+c=0$ no tiene soluciones, no podemos factorizar la función.
• Si la ecuación sólo tiene una solución, $x_1$, la forma factorizada es $f\left(x\right)=a(x-x_1{)}^2$

Ejemplo

En el ejemplo anterior vimos que los puntos de corte con el eje X de la función $f\left(x\right)=x^2-1$ son $(1,0)$ y $(-1,0)$. Por tanto, la forma factorizada de esta función es

ACTIVIDAD EN CASA:

Problema 1

Calcular el vértice de la siguiente función parabólica:

Problema 2

Determinar los puntos de corte y el vértice de la siguiente función: