Ciencias Exactas: CLASE DE MATEMATICA GRADO 11° DEL 2 DE OCTUBRE DEL 2024 SEM #30 TEMA: INDETERMINACIONES DE LA FORMA 0/0

	ÁREA: MATEMATICA	GRADO: 11°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL 2 DE OCTUBRE DEL 2024	PERIODO: CUARTO
	VALOR: LA AMISTAD Y LA PAZ	FRASE: "SOMOS INTEGRALES ASI NOS HIZO DIOSQUERIDOS AMIGOS OFRECE ESTA OPCION EDUCACION EN SABERES,VALOR Y FORMACION BUSCANDO EN NOSOTRO SIEMPRE LO MEJOR"

FECHA: DEL 2 DE OCTUBRE DEL 2024

GRADO: 11°

TEMA: INDETERMINACIONES DE LA FORMA 0/0

SUBTEMA: INDETERMINACIONES DE LA FORMA 0/0

LOGRO. Utiliza factorizaciones y racionalizaciones para hallar limites de funciones.

ACTIVIDAD PREVIA: Exploro mis conocimientos. "Discontinuidades evitables". lluvia de ideas.

EXPLORO PAGINA 95

INDETERMINACIONES DE LA FORMA 0/0

EJERCIOS PROPUESTOS A DESARROLLAR EN CLASE DOCENTE ESTUDIANES

Si el límite de una función racional produce una indeterminación del tipo 0/0 , entonces podemos recurrir a otros métodos para poder facilitar la solución de otras maneras, tal es el caso del uso de la factorización. Para ello podemos resumir en tres puntos el proceso para encontrar un nuevo resultado, no sin antes mencionar que este proceso se cumple para límites algebraicos indeterminados de la forma 0/0

Factorizar el numerador y el denominador
dividir los factores comunes
Luego reevaluar el límite

Ejercicios de Límites Indeterminados 0/0

Comencemos con los siguientes ejercicios.

Problema 1.- Evalúe el siguiente límite

$\displaystyle \underset{x\to -3}{\mathop{\lim }}\,\frac{{{x}^{2}}+x-6}{{{x}^{2}}+8x+15}$

Solución:

Paso 1: Confirmamos que el límite tiene una indeterminación:

$\displaystyle \underset{x\to -3}{\mathop{\lim }}\,\frac{{{x}^{2}}+x-6}{{{x}^{2}}+8x+15}=\frac{{{(-3)}^{2}}+(-3)-6}{{{(-3)}^{2}}+8(-3)+15}=\frac{9-9}{9-24+15}=\frac{0}{0}$

Paso 2: Ya que la función es racional, podemos intentar factorizar tanto el numerador como el denominador para identificar factores comunes.

$\displaystyle \underset{x\to -3}{\mathop{\lim }}\,\frac{{{x}^{2}}+x-6}{{{x}^{2}}+8x+15}=\underset{x\to -3}{\mathop{\lim }}\,\frac{(x+3)(x-2)}{(x+3)(x+5)}=\underset{x\to -3}{\mathop{\lim }}\,\frac{x-2}{x+5}$

Paso 3: Evaluando lo que nos quedó del límite:

$\displaystyle \underset{x\to -3}{\mathop{\lim }}\,\frac{x-2}{x+5}=\frac{-3-2}{-3+5}=\frac{-5}{2}=-\frac{5}{2}$

Respuesta:

$\displaystyle \underset{x\to -3}{\mathop{\lim }}\,\frac{{{x}^{2}}+x-6}{{{x}^{2}}+8x+15}=-\frac{5}{2}$

Problema 2.- Evalúe el siguiente límite

$\displaystyle \underset{x\to 4}{\mathop{\lim }}\,\frac{2{{x}^{2}}-7x-4}{{{x}^{3}}-8{{x}^{2}}+16x}$

Solución:

Paso 1: Confirmamos que el límite tiene una indeterminación:

$\displaystyle \underset{x\to 4}{\mathop{\lim }}\,\frac{2{{x}^{2}}-7x-4}{{{x}^{3}}-8{{x}^{2}}+16x}=\frac{2{{(4)}^{2}}-7(4)-4}{{{(4)}^{3}}-8{{(4)}^{2}}+16(4)}=\frac{0}{0}$

Como 0/0 es una forma indeterminada, el límite puede (o no) existir. Pero veamos el siguiente paso:

Paso 2: Dado que la función es racional, intente factorizar para encontrar cualquier factor común.

$\displaystyle \underset{x\to 4}{\mathop{\lim }}\,\frac{2{{x}^{2}}-7x-4}{{{x}^{3}}-8{{x}^{2}}+16x}=\underset{x\to 4}{\mathop{\lim }}\,\frac{(x-4)(2x+1)}{x(x-4)(x-4)}=\underset{x\to 4}{\mathop{\lim }}\,\frac{2x+1}{x(x-4)}$

Paso 3: Evaluando lo que nos queda del límite:

$\displaystyle \underset{x\to 4}{\mathop{\lim }}\,\frac{2x+1}{x(x-4)}=\frac{2(4)+1}{4(4-4)}=\frac{8+1}{4(0)}=\frac{9}{0}$

Observamos que el límite no existe.

Respuesta:

$\displaystyle \underset{x\to 4}{\mathop{\lim }}\,\frac{2{{x}^{2}}-7x-4}{{{x}^{3}}-8{{x}^{2}}+16x}=no\,existe$

Problema 3.- Evalúe el siguiente límite

Solución:

$\displaystyle \underset{x\to 2}{\mathop{\lim }}\,\frac{{{x}^{2}}+5x-14}{{{x}^{2}}-4}$

Paso 1: Confirmamos que el límite tiene una indeterminación:

$\displaystyle \underset{x\to 2}{\mathop{\lim }}\,\frac{{{x}^{2}}+5x-14}{{{x}^{2}}-4}=\frac{{{(2)}^{2}}+5(2)-14}{{{(2)}^{2}}-4}=\frac{4+10-14}{4-4}=\frac{0}{0}$

Paso 2: Factorizando tanto al numerador, como al denominador:

$\displaystyle \underset{x\to 2}{\mathop{\lim }}\,\frac{{{x}^{2}}+5x-14}{{{x}^{2}}-4}=\underset{x\to 2}{\mathop{\lim }}\,\frac{(x+7)(x-2)}{(x+2)(x-2)}=\underset{x\to 2}{\mathop{\lim }}\,\frac{x+7}{x+2}$

Paso 3: Evaluando lo que nos queda del límite:

$\displaystyle \underset{x\to 2}{\mathop{\lim }}\,\frac{x+7}{x+2}=\frac{2+7}{2+2}=\frac{9}{4}$

Respuesta:

$\displaystyle \underset{x\to 2}{\mathop{\lim }}\,\frac{{{x}^{2}}+5x-14}{{{x}^{2}}-4}=\frac{9}{4}$

Problema 4.- Evalúe el siguiente límite

$\displaystyle \underset{x\to -1}{\mathop{\lim }}\,\frac{{{x}^{2}}-4x-5}{{{x}^{2}}+10x+9}$

Solución:

Paso 1: Confirmamos que el límite tiene una indeterminación:

$\displaystyle \underset{x\to -1}{\mathop{\lim }}\,\frac{{{x}^{2}}-4x-5}{{{x}^{2}}+10x+9}=\frac{{{(-1)}^{2}}-4(-1)-5}{{{(-1)}^{2}}+10(-1)+9}=\frac{0}{0}$

Paso 2: Factorizando tanto al numerador, como al denominador:

$\displaystyle \underset{x\to -1}{\mathop{\lim }}\,\frac{{{x}^{2}}-4x-5}{{{x}^{2}}+10x+9}=\underset{x\to -1}{\mathop{\lim }}\,\frac{(x-5)(x+1)}{(x+9)(x+1)}=\underset{x\to -1}{\mathop{\lim }}\,\frac{x-5}{x+9}$

Paso 3: Evaluando lo que nos queda del límite:

$\displaystyle \underset{x\to -1}{\mathop{\lim }}\,\frac{x-5}{x+9}=\frac{-1-5}{-1+9}=\frac{-6}{8}=-\frac{6}{8}=-\frac{3}{4}$

Respuesta:

$\displaystyle \underset{x\to -1}{\mathop{\lim }}\,\frac{{{x}^{2}}-4x-5}{{{x}^{2}}+10x+9}=-\frac{3}{4}$

Problema 5.- Evalúe el siguiente límite

$\displaystyle \underset{x\to \frac{1}{3}}{\mathop{\lim }}\,\frac{3{{x}^{2}}-7x+2}{3{{x}^{2}}+5x-2}$

Solución:

Paso 1: Confirmamos que el límite tiene una indeterminación:

$\displaystyle \underset{x\to \frac{1}{3}}{\mathop{\lim }}\,\frac{3{{x}^{2}}-7x+2}{3{{x}^{2}}+5x-2}=\frac{3{{(\frac{1}{3})}^{2}}-7(\frac{1}{3})+2}{3(\frac{1}{3})+5(\frac{1}{3})-2}=\frac{0}{0}$

Paso 2: Factorizando tanto al numerador, como al denominador:

$\displaystyle \underset{x\to \frac{1}{3}}{\mathop{\lim }}\,\frac{3{{x}^{2}}-7x+2}{3{{x}^{2}}+5x-2}=\underset{x\to \frac{1}{3}}{\mathop{\lim }}\,\frac{(3x-1)(x-2)}{(3x-1)(x+2)}=\underset{x\to \frac{1}{3}}{\mathop{\lim }}\,\frac{x-2}{x+2}$

Paso 3: Evaluando lo que nos queda del límite:

$\displaystyle \underset{x\to \frac{1}{3}}{\mathop{\lim }}\,\frac{x-2}{x+2}=\frac{\frac{1}{3}-2}{\frac{1}{3}+2}=\frac{-\frac{5}{3}}{\frac{7}{3}}=-\frac{5}{7}$

Respuesta:

$\displaystyle \underset{x\to \frac{1}{3}}{\mathop{\lim }}\,\frac{3{{x}^{2}}-7x+2}{3{{x}^{2}}+5x-2}=-\frac{5}{7}$

Problema 6

Calcular el siguiente límite sin aplicar la regla de L'Hôpital:

En esta página hablamos sobre la indeterminación cero partido cero (0/0), viendo ejemplos y técnicas para evitar esta indeterminación (incluida la regla de L'Hôpital). Resolvemos límites con la indeterminación 0 dividido 0 paso a paso. Límites. Análisis de una variable. Matemáticas. Bachillerato y universidad.

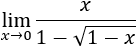
Tenemos la indeterminación 0 partido 0.

Como en el denominador tenemos una resta con una raíz, multiplicamos y dividimos la fracción por el conjugado del denominador:

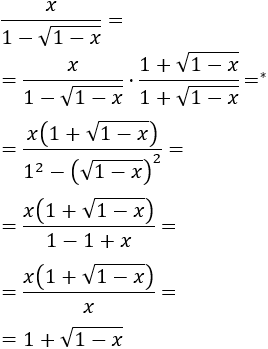
Nota*: hemos utilizado el producto notable suma por diferencia.

Por tanto, el límite es

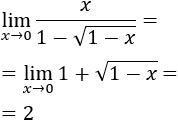
ACTIVIDAD EN CASA:

REALIZA LOS EJERCICIOS DEL 22 AL 31

Ciencias Exactas

PRINCIPAL

BIENVENIDA

miércoles, 2 de octubre de 2024

CLASE DE MATEMATICA GRADO 11° DEL 2 DE OCTUBRE DEL 2024 SEM #30 TEMA: INDETERMINACIONES DE LA FORMA 0/0

Ejercicios de Límites Indeterminados 0/0

Problema 6

No hay comentarios.:

Publicar un comentario