CLASE DE MATEMATICA GRADO 9° DEL 21 DE OCTUBRE DEL 2024 TEMA: ECUACION CUADRATICA

 

	ÁREA: MATEMATICA	GRADO: 9°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL 21  DE OCTUBRE DEL 2024	PERIODO: CUARTO
	VALOR: LA AMISTAD Y LA PAZ	FRASE:  "SOMOS INTEGRALES ASI NOS HIZO DIOSQUERIDOS AMIGOS OFRECE ESTA OPCION EDUCACION EN SABERES,VALOR Y FORMACION BUSCANDO EN NOSOTRO SIEMPRE LO MEJOR"

FECHA: DEL 21 DE SEPTIEMBRE DEL 2024

 GRADO: 9°

TEMA: ECUACION  CUADRATICA

SUBTEMA: ECUACION CUADRATICA POR FORMULA GENERAL

LOGRO: Soluciona ecuaciones cuadráticas y la aplica en la solución de problema.

ACTIVIDAD PREVIA: Exploro mis conocimientos. "Participemos en una feria". lluvia de ideas.

EXPLORO PAGINA 143 DEL LIBRO

 ECUACION CUADRATICA POR FORMULA GENERAL.

 Una fórmula general es una expresión que puede aplicarse para calcular el valor de una variable a partir de determinados datos.

Usualmente, con fórmula general se hace referencia a aquella que permite resolver ecuaciones cuadráticas, es decir, ecuaciones de segundo grado. Estas son aquellas donde el máximo exponente al que está elevada la incógnita es 2 y que tiene la siguiente forma:

ax2+bx+c=0

Tomando como referencia esta estructura, la fórmula general para resolver la ecuación es la siguiente

Como podemos observar, este tipo de ecuaciones tiene dos raíces o dos posibles soluciones, cada una de las cuales se puede calcular a partir de la misma fórmula, solo que cambiando un signo de suma por el de resta o viceversa en el numerador, entre -b y la raíz cuadrada de b2-4ac.

Ejemplo de fórmula general

Veamos mejor, con un ejemplo, la aplicación de la fórmula general de ecuaciones cuadráticas.

Si tenemos:

6x2-19x+7=0

Tomando como referencia la fórmula mostrada previamente, a=6, b=-19 y c=7.

Entonces, resolveremos de la siguiente manera:

Fórmula general en geometría

El concepto de fórmula general también puede ser aplicado en geometría, por ejemplo, para aquellas ecuaciones que permiten hallar valores específicos, como el perímetro o el área de una figura geométrica.

Por ejemplo, el perímetro (P) de un cuadrado se halla multiplicando el lado (L) por 4, es decir, P=4L. Asimismo, el área(A) de un cuadrado es igual al lado elevado al cuadrado, es decir, la fórmula general del área de esta figura geométrica es A=L2. Esto se cumple para todos los cuadrados, que son paralelogramos con cuatro lados de igual longitud y paralelos entre sí.

De igual modo, la fórmula general del área de un triángulo es A=1/2*b*h. Es decir, el área es igual a 1/2 por la base y por la altura de la figura.

Este tipo de fórmulas nos permiten hallar ciertas medidas o datos de la figura, y también las encontramos en el caso de las figuras tridimensionales. Por ejemplo, el volumen (V) de un cubo es igual a la arista (a) al cubo. Es decir, V=a3.

Debemos recordar en este punto que la arista es aquel segmento que une dos caras de la figura y que el cubo es un poliedro regular con seis caras todas iguales, cada una de las cuales es un cuadrado.

EJERCICIO.

1. Resolver la ecuación de segundo grado completa

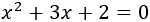
Resolvemos:

Es una ecuación completa con coeficientes $a=1$, $b=3$ y $c=2$. Aplicamos la fórmula:

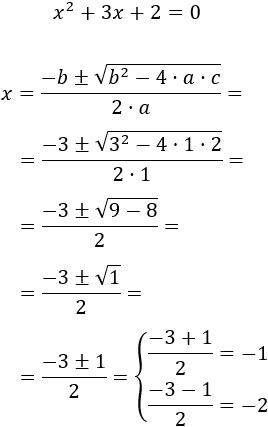
Por tanto, las soluciones son -1 y -2.

2. Resolver la ecuación completa

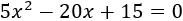
Resolvemos:

Es una ecuación completa con coeficientes $a=5$, $b=-20$ y $c=15$. Aplicamos la fórmula:

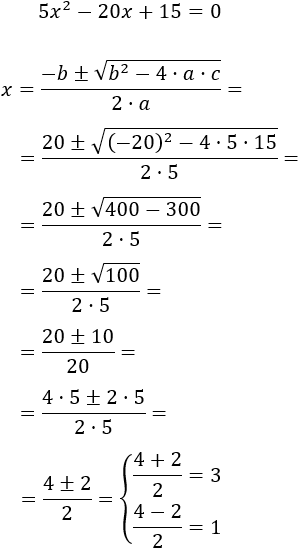
Las soluciones de la ecuación son $3$ y $1$.

ACTIVIDAD EN CASA:

RESUELVE LA PAGINA 146 PUNTOS DE LOS EJERCICIOS 26 AL 35 POR FORMULA GENERAL