CLASE DE LOGICA Y ESTADISTICA GRADO 11° DEL 14 DE FEBRERO DEL 2024 SEMANA #2 TEMA PROPOSICIONES SIMPLES Y COMPUESTAS

	ÁREA:  LOGICA Y ESTADISTICA	GRADO: 11°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL 14 DE FEBRERO DEL 2024	PERIODO: PRIMERO
	VALOR: RESPETO	FRASE: “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION”

FECHA: DEL 14  DE FEBRERO DEL 2024

 GRADO: 11°

TEMA: PROPOSICIONES

SUBTEMA:  PROPOSICIONES SIMPLES Y COMPUESTAS

LOGRO. Reconoce  la lógica y las proposiciones para aplicarla en la vida cotidiana.

ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿Qué una proposición simple?. lluvia de ideas.

LÓGICA MATEMÁTICA

PROPOSICION:

PROPOSICION SIMPLE O ATOMICA:

Son aquellas que no poseen operador lógico

alguno.

p: Todos los triángulos son isósceles. (F)

q: 8 es un número par. (V)

r: 2 es el inverso multiplicativo de –2. (V)

PROPOSICION COMPUESTA O MOLECULAR:

Son aquellas que poseen operador lógico.

Si 3 es impar entonces 3 es menor que 6.

p: El número 3 es impar

q: El número 3 es menor que el número 6

p → q

Un triángulo es equilátero si y solo si tiene sus

tres lados iguales

p: Un triángulo es equilátero

q: Un triángulo tiene sus tres lados iguales

p ↔ q

CONECTORES:

La siguiente tabla muestra algunos de los conectivos más utilizados en la lógica proposicional con su respectivo nombre, símbolo, notación y lectura

DEFINICION:

(Conectivos Lógicos) Se definen los conectivos lógicos:

1. ∧: Conjunción ("y")

2. ∨: Disyunción ("o").

 3. ⊻: Disyunción Exclusiva ("o bien").

4. ⇒: Implicancia ("entonces").

5. ⇔: Equivalencia ("si y sólo si").

DEFINICION CONJUNCION.

(Conjunción, "y lógico") Dados p, q; dos proposiciones lógicas, se construye su conjunción como (p∧q) Se lee: p y q

(p∧q) es verdadera si p y q son simultáneamente verdaderas. En los demás casos, es falsa. La conjunción posee la tabla de verdad

 

p	q	(p∧q)
V	V	V
V	F	F
F	V	F
F	F	F

DISYUNCION:

(Disyunción, "o lógico") Dados p, q; dos proposiciones lógicas, se construye su disyunción como (p∨q). Se lee: p o q

(p∨q) es falsa si p y q son simultáneamente falsas. En los demás casos, es verdadera. La disyunción posee la tabla de verdad 

p	q	(p∨q)
V	V	V
V	F	V
F	V	V
F	F	F

DISYUNCION EXCLUSIVA:

(Disyunción Exclusiva, "o bien") Dados p, q; dos proposiciones lógicas, se construye su disyunción exclusiva como. (p⊻q). Se lee: p o bien q.

(p⊻q) es falsa si p y q tienen el mismo valor de verdad. En caso contrario, es verdadera. La disyunción exclusiva posee la tabla de verdad

p	q	(p⊻q)
V	V	F
V	F	V
F	V	V
F	F	F

IMPLICACION:

(Implicancia, "entonces") Dados p, q; dos proposiciones lógicas, se construye su implicancia como (p⇒q). Se lee: p entonces q.

(p⇒q) es falsa si q es falsa. En los demás casos, es verdadera. La implicancia posee la tabla de verdad

p	q	(p⇒q)
V	V	V
V	F	F
F	V	V
F	F	V

EQUIVALENCIA O DOBLE IMPLICACION:

(Equivalencia, "si y sólo si") Dados p, q; dos proposiciones lógicas, se construye su equivalencia como (p⇔q). Se lee: p si y sólo si q.

(p⇔q) es verdadera si p y q tienen el mismo valor de verdad. En caso contrario, es falsa. La equivalencia posee la tabla de verdad

p	q	(p⇔q)
V	V	V
V	F	F
F	V	F
F	F	V

ACTIVIDAD EN CASA:

REALIZA 10 PROPOSICIONES ATOMICAS Y 10 MOLECULARES.

ESTADISTICA:

VARIABLE ESTADISTICA  BIDIMENCIONAL.

Una distribución bidimensional es aquella en las que a cada individuo le corresponden los valores de dos variables, las representamos por el par (xi, yi).

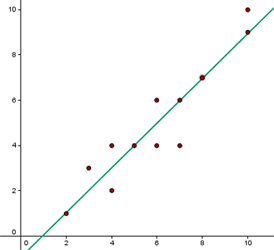
Si representamos cada par de valores como las coordenadas de un punto, el conjunto de todos ellos se llama nube de puntos o diagrama de dispersión.

Sobre la nube de puntos puede trazarse una recta que se ajuste a ellos lo mejor posible, llamada recta de regresión.

EJEMPLO

Las notas de 12 alumnos de una clase en Matemáticas y Física son las siguientes:

Matemáticas	Física
2	1
3	3
4	2
4	4
5	4
6	4
6	6
7	4
7	6
8	7
10	9
10	10

COVARIANZA:

La covarianza de una variable bidimensional es la media aritmética de los productos de las desviaciones de cada una de las variables respecto a sus medias respectivas.

La covarianza se representa por sxy o σxy.

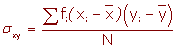
La covarianza indica el sentido de la correlación entre las variables

Si σxy >0 la correlación es directa.

Si σxy <0 la correlación es inversa.

La covarianza presenta como inconveniente, el hecho de que su valor depende de la escala elegida para los ejes.

Es decir, la covarianza variará si expresamos la altura en metros o en centímetros. También variará si el dinero lo expresamos en euros o en dólares.

CORRELACION:

La correlación determina la relación o dependencia que existe entre las dos variables que intervienen en una distribución bidimensional.

Es decir, determinar si los cambios en una de las variables influyen en los cambios de la otra. En caso de que suceda, diremos que las variables están correlacionadas o que hay correlación entre ellas.

COEFICIENTE DE CORRELACION:

El coeficiente de correlación lineal se expresa mediante la letra r.

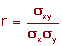
EJERCICIO PROPUESTO PARA TRABAJAR EN CLASE Y CASA :

1. Una compañía de seguros considera que el número de vehículos (y) que circulan por una determinada autopista a más de 120 km/h , puede ponerse en función del número de accidentes (x) que ocurren en ella. Durante 5 días obtuvo los siguientes resultados:

Accidentes xi	5	7	2	1	9
Vehículos yi	15	18	10	8	20

  a) Calcula el coeficiente de correlación lineal.

  b) Si ayer se produjeron 6 accidentes, cuántos vehículos podemos suponer que circulaban por la autopista a más de 120 km/h?

  c) ¿Es buena la predicción?

Construimos una tabla con las columnas necesarias

Vemos las fórmulas que tenemos que aplicar para saber las columnas que necesitamos, a continuación se explica la forma de hacer esto.