ÁREA: EST Y LOG | GRADO: 8° | |
DOCENTE: ENAIDO MALDONADO POLO | CORREO: matematica. ceqa@gmail.com | |
FECHA: DEL 16 DE SEPT DEL 2024 | PERIODO: CUARTO | |
VALOR: RESPONSABILIDAD | FRASE: "SOMOS INTEGRALES ASI NOS HIZO DIOSQUERIDOS AMIGOS OFRECE ESTA OPCION EDUCACION EN SABERES,VALOR Y FORMACION BUSCANDO EN NOSOTRO SIEMPRE LO MEJOR" |
FECHA: DEL 16 DE SEPT DEL 2024
GRADO: 8°
TEMA: MEDIDAS DE DISPERSION
SUBTEMA: VARIANZA
LOGRO. En un conjunto de datos determina las medidas de dispersión que los caracterizan
NOTA: CONTINUIDAD CLASE ANTERIOR (EXPLICASION)
ACTIVIDAD PREVIA: Exploro mis conocimientos. "festejando un nuevo año" Exploro pagina 322
MEDIDAS DE DISPERSION
Donde:
es la variable aleatoria de la que se quiere calcular la varianza.
es el valor del dato
.
es el número total de observaciones.
es la media de la variable aleatoria
.
Puedes usar la calculadora que hay más abajo para calcular la varianza de cualquier conjunto de datos.
Por lo tanto, para sacar la varianza de una serie de datos es indispensable que sepas cómo se calcula la media aritmética. Si no recuerdas cómo se hace, puedes repasarlo en el artículo enlazado más arriba.
Ejemplo de la varianza
Ahora que ya sabemos la definición de varianza, vamos a resolver un ejercicio paso a paso para que veas cómo se saca la varianza de una serie de datos.
- De una empresa multinacional se conoce el resultado económico que ha tenido durante los últimos cinco años, en la mayoría ha obtenido beneficios pero un año presentó unas pérdidas considerables: 11, 5, 2, -9, 7 millones de euros. Calcula la varianza de este conjunto de datos.
Como hemos visto en la explicación de arriba, lo primero que debemos hacer para hallar la varianza de una serie de datos es calcular su media aritmética:
Y una vez sabemos el valor promedio de los datos podemos utilizar la fórmula de la varianza:
Sustituimos los datos proporcionados por el enunciado del ejercicio en la fórmula:
Por último, solo queda resolver las operaciones para hacer el cálculo de la varianza:
Fíjate que las unidades de la varianza son las mismas unidades de los datos estadísticos pero elevadas al cuadrado, por eso la varianza de este grupo de datos es 45,76 millones de euros2.
Ejemplo 3:
Calcular la varianza y la desviación estándar de los siguientes datos: 1, 3, 5, 7 y 9 sabiendo que corresponden a una muestra
Solución:
Nos indican que estos datos forman una muestra, por lo tanto, usaremos las fórmulas de varianza y desviación estándar para la muestra, teniendo en cuenta que tenemos 5 datos, es decir, n = 5.
Empezamos calculando la media de la muestra:

Ahora calculamos la varianza de la muestra:

El valor de la varianza poblacional, es de 10.
Ahora calculamos la desviación estándar, teniendo en cuenta que es la raíz cuadrada de la varianza.
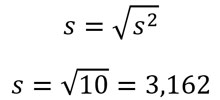
Considérese los siguientes datos:  . Se pide:
. Se pide:
Calcular su media y su varianza.
LOGICA
LOGICA:TEMA: LOS PORCENTAJESSUBTEMA: REGLA DE TRES LOGRO. Aplica la regla de tres para desarrollar situaciones de problemas.REGLA DE TRES Regla de tres compuesta inversaUna regla de tres compuesta inversa se compone de varias reglas de tres simples inversas aplicadas sucesivamente

Si la magnitud en la primera columna aumenta (o disminuye), entonces disminuye (o aumenta) en la tercera columna; si la magnitud en la segunda columna aumenta (o disminuye), entonces disminuye (o aumenta) en la tercera columna. La fórmula a emplear es

Ejemplo de problema con la regla de tres compuesta inversa
 obreros trabajando, trabajando
obreros trabajando, trabajando  horas diarias construyen un muro en
horas diarias construyen un muro en  días. ¿Cuánto tardarán
días. ¿Cuánto tardarán 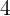 obreros trabajando
obreros trabajando  horas diarias?
horas diarias?
1. Planteamos por columnas

Si la magnitud en la primera columna aumenta (o disminuye), entonces disminuye (o aumenta) en la tercera columna; si la magnitud en la segunda columna aumenta (o disminuye), entonces disminuye (o aumenta) en la tercera columna. La fórmula a emplear es

Ejemplo de problema con la regla de tres compuesta inversa
 obreros trabajando, trabajando
obreros trabajando, trabajando  horas diarias construyen un muro en
horas diarias construyen un muro en  días. ¿Cuánto tardarán
días. ¿Cuánto tardarán 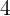 obreros trabajando
obreros trabajando  horas diarias?
horas diarias?
1. Planteamos por columnas

2. Verificamos que sea inversa

3. Aplicamos la fórmula de regla de tres compuesta inversa

de donde se obtiene
 días
días
Regla de tres compuesta mixta
Una regla de tres compuesta mixta se compone de varias reglas de tres simples directas e inversas aplicadas sucesivamente

2. Verificamos que sea inversa

3. Aplicamos la fórmula de regla de tres compuesta inversa

de donde se obtiene
 días
días
Regla de tres compuesta mixta
Una regla de tres compuesta mixta se compone de varias reglas de tres simples directas e inversas aplicadas sucesivamente

Si la primera y tercera columna es una regla de tres simple directa, mientras que la segunda y tercera columna es una regla de tres simple inversa, entonces se tiene

Ejemplo de problema con la regla de tres compuesta mixta
Si  obreros realizan en
obreros realizan en  días trabajando a razón de
días trabajando a razón de  horas por día un muro de
horas por día un muro de 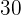 m. ¿Cuántos días necesitarán
m. ¿Cuántos días necesitarán  obreros trabajando
obreros trabajando  horas diarias para realizar los
horas diarias para realizar los  m de muro que faltan?
m de muro que faltan?
1. Planteamos por columnas

Si la primera y tercera columna es una regla de tres simple directa, mientras que la segunda y tercera columna es una regla de tres simple inversa, entonces se tiene

Ejemplo de problema con la regla de tres compuesta mixta
Si  obreros realizan en
obreros realizan en  días trabajando a razón de
días trabajando a razón de  horas por día un muro de
horas por día un muro de 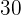 m. ¿Cuántos días necesitarán
m. ¿Cuántos días necesitarán  obreros trabajando
obreros trabajando  horas diarias para realizar los
horas diarias para realizar los  m de muro que faltan?
m de muro que faltan?
1. Planteamos por columnas

2. Verificamos las reglas de tres simples

3. Aplicamos la regla de tres compuesta mixta

de donde se obtiene
 días
días
ACTIVIDAD EN CASA:
PLANTEA UN PROBLEMA Y APLICA LA REGLA DE TRES INVERSA PARA SOLUCIONARLO.

2. Verificamos las reglas de tres simples

3. Aplicamos la regla de tres compuesta mixta

de donde se obtiene
 días
días
ACTIVIDAD EN CASA:
PLANTEA UN PROBLEMA Y APLICA LA REGLA DE TRES INVERSA PARA SOLUCIONARLO.




No hay comentarios.:
Publicar un comentario