ÁREA: EST Y LOG | GRADO: 8° | |
DOCENTE: ENAIDO MALDONADO POLO | CORREO: matematica. ceqa@gmail.com | |
FECHA: DEL 30 DE SEPT DEL 2024 | PERIODO: CUARTO | |
VALOR: LA AMISTAD Y LA PAZ | FRASE: "Logramos nuestras metas, salimos adelante con un futuro serio, social y responsable. Nosotros orgullosos nos llenamos de gloria llegamos como niños, crecemos en victoria." |
FECHA: DEL 30 DE SEPT DEL 2024
GRADO: 8°
TEMA: MEDIDAS DE DISPERSION
SUBTEMA: DESVIACION TIPICA
LOGRO. En un conjunto de datos determina las medidas de dispersión que los caracterizan
ACTIVIDAD PREVIA: Exploro mis conocimientos. "festejando un nuevo año" Exploro pagina 322
MEDIDAS DE DISPERSION
Desviación típica
La desviación típica es otra medida que ofrece información de la dispersión respecto a la media. Su cálculo es exactamente el mismo que la varianza, pero realizando la raíz cuadrada de su resultado. Es decir, la desviación típica es la raíz cuadrada de la varianza.

- X → Variable sobre la que se pretenden calcular la varianza
- xi → Observación número i de la variable X. i puede tomará valores entre 1 y n.
- N → Número de observaciones.
- x̄ → Es la media de la variable X.
- Es decir, primero calculamos la media y elevamos al cuadrado la diferencia entre cada valor y ese promedio.¿Por qué elevar al cuadrado? Pues, al no hacerlo, aquellos datos negativos y positivos, al sumarse, podrían eliminarse entre sí. Para entenderlo, veamos un ejemplo muy simple con las siguientes cifras:8,6,9,5,7Primero calculamos el promedio: (8+6+9+5+7)/5=35/5=7Luego, las diferencias respecto a cada dato son:8-7=16-7=-19-7=25-7=-27-7=0Si sumamos estas diferencias, el resultado es cero:1+(-1)+2+(-2)+0=0Pero, evidentemente, no es que el conjunto de datos no presente ninguna desviación. Por lo tanto, elevaremos al cuadrado las diferencias y calcularemos el promedio aritmético entre ellas, tal como indica la fórmula:
 Asimismo, para datos agrupados la fórmula sería la siguiente, donde f es la frecuencia o el número de veces que se repite la observación:
Asimismo, para datos agrupados la fórmula sería la siguiente, donde f es la frecuencia o el número de veces que se repite la observación:Cómo usar paso a paso las fórmulas de la desviación estándar
Para ilustrar mejor cómo utilizar cada término de la fórmula, veamos un ejemplo. Tomemos el siguiente conjunto de valores: 5, 9, 12 y 15. Teniendo en cuenta estos valores, el primer paso es calcular la media de los mismos.
Primer paso: calcula la media de los valores
Para saber cuál es la media aritmética de todos los valores o x̄, basta con sumar los valores observados y dividirlos por el número de datos.
Con el valor promedio ya obtenido, procedamos a calcular el valor de la sumatoria.
Segundo paso: calcula el valor de la sumatoria
Para conocer el valor de la sumatoria, hemos de sumar los cuadrados de las diferencias entre los datos y la media. Es decir:
Ahora que conocemos el valor de la sumatoria, procedamos con el cálculo de la varianza.
Tercer paso: calcula la varianza
Para calcular la varianza, precisamos aplicar la división de la fórmula. Esto cambiará dependiendo de si buscamos obtener la desviación estándar de toda una población o la de una muestra.
Si el conjunto de valores 5, 9, 12 y 15 representan a toda una población, entonces:
Si el conjunto de valores 5, 9, 12 y 15 es una muestra y no representan a toda una población, entonces:
La varianza es el cuadrado de la desviación estándar. Por esta razón, queda un paso más para obtener la desviación estándar de una población o muestra.
Cuarto paso: obtén la desviación estándar a partir de la varianza
Para terminar, solo nos queda aplicar la raíz cuadrada a la varianza y obtener así la desviación estándar.
La desviación estándar poblacional en este ejemplo es:
La desviación estándar muestral en este ejemplo es:
Como vemos en el ejemplo, la desviación estándar de una muestra (4,27) es mayor a la de la población (3,7). Esto siempre será así, ya que, en el caso de una muestra, el denominador de la división (N–1) es menor a cuando se calcula la desviación de una población (N).
- ACTIVIDAD EN CASA:
LOGICA
LOGICA:FECHA: DEL 30 DE SEPT DEL 2024
GRADO: 8°
TEMA: INTERES SIMPLE E INTERES COMPUESTO
SUBTEMA: INTERES SIMPLE E INTERES COMPUESTO
LOGRO. Aplica el interés simple y compuesto para desarrollar situaciones de problemas cotidianos.
ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿Qué es regla de tres?. lluvia de ideas.INTERES SIMPLE E INTERES COMPUESTOInterés Simple y CompuestoInterés Simple
FECHA: DEL 30 DE SEPT DEL 2024
GRADO: 8°
TEMA: INTERES SIMPLE E INTERES COMPUESTO
SUBTEMA: INTERES SIMPLE E INTERES COMPUESTO
LOGRO. Aplica el interés simple y compuesto para desarrollar situaciones de problemas cotidianos.
Es el interés o beneficio que se obtiene de una inversión de una empresa cuando los intereses producidos durante cada periodo de tiempo que dura la Inversión se deben únicamente al capital inicial, ya que los beneficios o intereses se retiran al vencimiento de cada uno de los periodos. Los periodos de tiempo pueden ser años, trimestres, meses... En resumen, el interés se aplica a la cantidad inicial, los intereses no se agregan al capital productivo.
Interés compuesto
El interés compuesto representa la acumulación de intereses que se han generado en un período determinado por un capital inicial (CI) o principal a una tasa de interés (r) durante (n) periodos de imposición, de modo que los intereses que se obtienen al final de cada período de inversión no se retiran sino que se reinvierten o añaden al capital inicial, es decir, se capitalizan.
EJERCICIOS DE CALCULO DE INTERES:
¿Durante cuánto tiempo ha de imponerse un capital de 25 00 convierta en 30 000 €?
SOLUCION: Notemos tanto, primero debemos calcular el interés que debemos obtener:
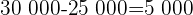 €Una vez que tenemos el interés que deseamos obtener, entonces calculamos el tiempo utilizando:
€Una vez que tenemos el interés que deseamos obtener, entonces calculamos el tiempo utilizando:
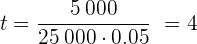
Por lo tanto, el tiempo requerido es 4 años.
Ejercicios
1. Calcula el beneficio obtenido de un capital de 5 000€ colocado al 2,5% anual durante 7 meses.
2. Un agricultor compra una finca de 24 hm2 a 1,2 € el metro cuadrado, acordando saldar su deuda tres años más tarde con un interés del 3% anual. ¿Qué cantidad deberá aportar al cabo de 3 años?
3. ¿En cuánto se transforma un capital de 100 000 € colocado al 3,6 % anual durante 3 años?
4. ¿En cuánto se transforma un capital de 100 000 € colocado al 0,3 % mensual durante 3 meses?
5. ¿Qué beneficio obtiene un prestamista que cede un capital de 2 500 €, al 12 % anual durante 45 días?
6. Un banco cobra un interés del 19 % anual por los descubiertos en las cuentas ¿Qué coste tiene para un cliente haber dejado su cuenta con un déficit de 75 € durante 15 días?
7. ¿Qué renta mensual obtiene un inversionista que coloca un capital de 18 500 €, al 6'25 %, durante 30 días?
8. ¿En cuánto se convertirá un capital de 80 000 €, colocado al 4 % anual, si se mantienen en el banco durante 3 años sin retirar los intereses?
9. Calcula el beneficio conseguido por un capital de 20 000 € colocado durante 2 años al 5% de interés compuesto anual.
10. Se colocan en el banco 3 400 €, al 2,5% de interés compuesto anual, durante 3 años. ¿Qué cantidad se retirará al final del periodo?
Es el interés o beneficio que se obtiene de una inversión de una empresa cuando los intereses producidos durante cada periodo de tiempo que dura la Inversión se deben únicamente al capital inicial, ya que los beneficios o intereses se retiran al vencimiento de cada uno de los periodos. Los periodos de tiempo pueden ser años, trimestres, meses... En resumen, el interés se aplica a la cantidad inicial, los intereses no se agregan al capital productivo.
El interés compuesto representa la acumulación de intereses que se han generado en un período determinado por un capital inicial (CI) o principal a una tasa de interés (r) durante (n) periodos de imposición, de modo que los intereses que se obtienen al final de cada período de inversión no se retiran sino que se reinvierten o añaden al capital inicial, es decir, se capitalizan.
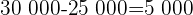 €
€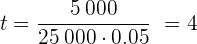
1. Calcula el beneficio obtenido de un capital de 5 000€ colocado al 2,5% anual durante 7 meses.
2. Un agricultor compra una finca de 24 hm2 a 1,2 € el metro cuadrado, acordando saldar su deuda tres años más tarde con un interés del 3% anual. ¿Qué cantidad deberá aportar al cabo de 3 años?
3. ¿En cuánto se transforma un capital de 100 000 € colocado al 3,6 % anual durante 3 años?
4. ¿En cuánto se transforma un capital de 100 000 € colocado al 0,3 % mensual durante 3 meses?
5. ¿Qué beneficio obtiene un prestamista que cede un capital de 2 500 €, al 12 % anual durante 45 días?
6. Un banco cobra un interés del 19 % anual por los descubiertos en las cuentas ¿Qué coste tiene para un cliente haber dejado su cuenta con un déficit de 75 € durante 15 días?
7. ¿Qué renta mensual obtiene un inversionista que coloca un capital de 18 500 €, al 6'25 %, durante 30 días?
8. ¿En cuánto se convertirá un capital de 80 000 €, colocado al 4 % anual, si se mantienen en el banco durante 3 años sin retirar los intereses?
9. Calcula el beneficio conseguido por un capital de 20 000 € colocado durante 2 años al 5% de interés compuesto anual.
10. Se colocan en el banco 3 400 €, al 2,5% de interés compuesto anual, durante 3 años. ¿Qué cantidad se retirará al final del periodo?














No hay comentarios.:
Publicar un comentario