ÁREA: MATEMATICA | GRADO: 7° | |
DOCENTE: ENAIDO MALDONADO POLO | CORREO: matemática. ceqa@gmail.com | |
FECHA: DEL 24 DE SEPT DEL 2024 | PERIODO: CUARTO | |
VALOR: LA AMISTAD Y LA PAZ | FRASE: "SOMOS INTEGRALES ASI NOS HIZO DIOSQUERIDOS AMIGOS OFRECE ESTA OPCION EDUCACION EN SABERES,VALOR Y FORMACION BUSCANDO EN NOSOTRO SIEMPRE LO MEJOR" |
FECHA: DEL 24 DE SEPT DEL 2024
GRADO: 7°
TEMA: ECUACIONES
SUBTEMA: ECUACIONES ARITMETICAS
LOGRO. Manipula expresiones lineales las presenta usando gráficos o tablas y las usa para modelar situaciones.
CTIVIDAD PREVIA: Exploro mis conocimiento "Pintando las paredes de la casa". lluvia de ideas.
exploro página 122. en clase.
ECUACIONES CON RACIONALES.
Las ecuaciones racionales son aquellas donde aparecen fracciones algebraicas y por tanto, la incógnita también aparece en el denominador.
Por ejemplo:
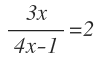
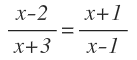

Como has podido comprobar en estos ejemplos, las ecuaciones racionales son ecuaciones con x en el denominador
¿Cómo se resuelven las ecuaciones racionales? Pues es lo que veremos en el siguiente apartado.
COMO SE RESUELVEN LAS ECUACIONES RACIONALES.
Para resolver este tipo de ecuaciones, debemos conseguir que la incógnita deje de estar en el denominador, para que podemos despejarla.
Para ello, lo que tenemos que hacer es pasar el denominador multiplicando al miembro contrario. De esta forma, el denominador desaparecerá y la incógnita ya no estará en el denominador y podremos despejarla sin problemas.
Por ejemplo:

Tenemos la x, tanto en el numerador como en el denominador. Pasamos el denominador del primer miembro multiplicando al segundo miembro. Como está dividiendo al numerador, pasa multiplicando al segundo miembro:
![]()
Ahora ya no tenemos denominadores y nos ha quedado una ecuación de primer grado, que seguimos resolviendo.
Eliminamos el paréntesis que tenemos en el segundo miembro multiplicando por el 2 que tiene delante:
![]()
Pasamos los términos con x a un miembro y los términos sin x al otro término:
![]()
Por último, despejamos la x:
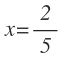
En la ecuación que acabamos de resolver, tan sólo teníamos una fracción algebraica en un miembro, es decir, teníamos la x en el denominador sólo en uno de los miembros.
Vamos a ver ahora cómo resolver ecuaciones racionales cuando tenemos fracciones algebraicas en ambos miembros o lo que es lo mismo, la x se encuentra en el denominador de ambos miembros, como por ejemplo:
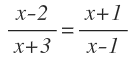
En esta ecuación tenemos la x tanto en el denominador tanto en el primer miembro como en el segundo miembro.
Para eliminar ambos denominadores, tenemos que multiplicar en cruz, es decir, el denominador del primer miembro pasa multiplicando al segundo miembro y el denominador del segundo miembro pasa multiplicando al primero. La ecuación nos queda de la siguiente forma:
![]()
Pasamos a tener una ecuación sin denominadores, donde para despejar la x, debemos eliminar los paréntesis multiplicando término a término:
![]()
Nos queda una ecuación de segundo grado. Para resolverla, pasamos todos los términos a un miembro e igualamos al ecuación a cero:
![]()
En este caso, al agrupar términos vemos que los términos de segundo grado se anulan , quedando una ecuación de primer grado:
![]()
Donde finalmente despejamos la x:
![]()
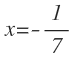
Como ves, el paso clave para resolver ecuaciones racionales es pasar multiplicando el denominador al otro miembro, tanto si tenemos la x en el denominador en uno o en los dos miembros.
Después, en función de la ecuación, debemos ir operando con paréntesis y resolver la ecuación de primer o de segundo grado que nos quede en cada caso.
EJERCICIOS RESUELTOS DE ECUACIONES RACIONALES.
Vamos a resolver ahora ecuaciones racionales donde antes de pasar el denominador multiplicando al otro miembro, es necesario operar con fracciones algebraicas, para tener una única fracción algebraica en cada miembro, como las ecuaciones del apartado anterior. Por ejemplo esta ecuación:
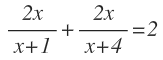
En este caso, para poder pasar el denominador multiplicando al otro miembro, antes hay que sumar las fracciones algebraicas. Si necesitas ayuda para operar con fracciones algebraicas, lo tienes explicado paso a paso.
Tenemos que sumar dos fracciones algebraicas con distinto denominador. Para ello debemos reducirlas a común denominador, obteniendo el mínimo común múltiplo de los denominadores:
![]()
Las sumamos por tanto, reduciendo a denominador común:
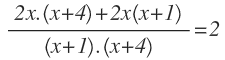
Operamos en el numerador y en el denominador para eliminar los paréntesis:

Agrupamos términos semejantes:
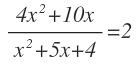
Ahora ya tenemos una sola fracción algebraica, por lo que podemos pasar el denominador del primer miembro multiplicando al 2 del segundo miembro:
![]()
Multiplicamos el 2 por el paréntesis para eliminarlo:
![]()
Nos queda una ecuación de segundo grado. Para resolverla, pasamos todos los términos a un miembro, igualando la ecuación a cero y agrupamos términos semejantes:
![]()
Tenemos una ecuación de segundo grado incompleta, que para resolverla, despejamos primero x al cuadrado:
![]()
Y después pasamos el cuadrado al otro miembro como raíz cuadrada:
![]()
Obteniendo dos soluciones, una positiva y otra negativa:
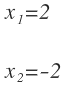
Atención a este paso que viene a continuación porque es muy importante: cuando operamos para reducir dos o más fracciones a común denominador, puede que estemos añadiendo una solución virtual a la ecuación que realmente no es una solución de la ecuación original y por tanto, se deben comprobar cada una de la soluciones para descartar la que no lo sea.
Para comprobar si una solución es válida o no, debemos sustituir la x por su valor en la ecuación original y ver si se cumple la igualdad. Si la igualdad se cumple, entonces la solución será válida y no será válida en caso contrario.
Sustituimos la x por 2:

Operamos para comprobar si se cumple la igualdad:
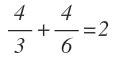
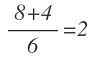
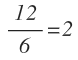
![]()
Si se cumple, por lo que x=2 es una solución válida.
Hacemos lo mismo con x=-2:
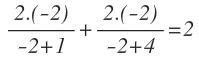
Operamos:

![]()
![]()
Con x=-2, también se cumple la igualdad, por lo que también es una solución válida.
Se puede dar el caso que la ecuación racional no tenga solución o que sólo tenga una solución
ACTIVIDAD EN CASA:
RESUELVE LOS SIGUIENTES EJERCICIOS.
Ejercicios propuestos
Resuelve las siguientes ecuaciones racionales:




No hay comentarios.:
Publicar un comentario