CLASE DE LOGICA Y ESTADISTICA GRADO 11° DEL 16 DE OCTUBRE DEL 2024 SEMANA # 35 TEMA: MEDIDAS DE PESO Y MASA

 

	ÁREA:  LOGICA Y ESTADISTICA	GRADO: 11°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL  16  DE  OCTUBRE DEL 2024	PERIODO: CUARTO
	VALOR:   LA AMISTAD Y  LA  PAZ	FRASE:   "SOMOS INTEGRALES ASI NOS HIZO DIOSQUERIDOS AMIGOS OFRECE ESTA OPCION EDUCACION EN SABERES,VALOR Y FORMACION BUSCANDO EN NOSOTRO SIEMPRE LO MEJOR"

FECHA: DEL 16 DE  OCTUBRE DEL 2024

 GRADO: 11°

TEMA: COVERSION DE UNIDADES DE LONGITUD.

SUBTEMA:  PROBLEMAS CON UNIDADES DE MEDIDAS

LOGRO. Reconoce  las medidas de longitud las aplica en situaciones cotidianas

ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿Qué una medida de peso?. lluvia de ideas.

CONTINUIDAD CLASE ANTERIOR:

LOGICA

Conversión de unidades de longitud

La longitud es una magnitud que permite expresar la distancia que existe entre dos puntos. En el Sistema Internacional de Unidades, la unidad de la longitud es el metro, pero existen otras unidades que nos permiten expresar longitudes. Aquí veremos como realizar conversiones, y pasar longitudes de un sistema a otro.

Equivalencias de longitud

• 1 metro = 3,28084 pies = 39,3701 pulgadas.
• 1 pulgada = 2,54 centímetros = 0,0254 metros.
• 1 pie = 12 pulgadas = 30,48 centímetros = 0,3048 metros.
• 1 milla = 5280 pies = 1,60 934 kilómetros = 1609,34 metros.
• 1 yarda =  3 pies = 36 pulgadas = 0,9144 metros.
• 1 metro = 100 centímetros.
• 1 kilómetro = 1000 metros = 1,904 yardas = 0,6215 millas.
• 1 angstrom = 10-8 centímetros.

Tabla de prefijos del Sistema Internacional de Unidades

Además de las equivalencias entre diferentes unidades de longitudes, la tabla de prefijos nos sacará de muchos apuros. Los prefijos nos permiten expresar cantidades muy grandes o muy pequeñas de una manera práctica.

Conversión de unidades

Para convertir unidades, vamos a revisar 2 métodos:

• Método de la regla de tres: este método es un clásico, lento pero seguro.
• Método del factor de conversión: el factor de conversión es una fracción, en la cual el numerador, es igual al denominador.

Veamos algunos ejemplos:

Ejemplo 1:

Convertir 3 metros (m) a pulgadas (in).

Solución usando regla de tres:

Usaremos la clásica regla de tres, teniendo en cuenta que 1 metro = 39,3701 pulgadas (in).

Solución usando un factor de conversión:

Con el método del factor de conversión, solo necesitamos saber que 1 metro = 39,3701 pulgadas (in).

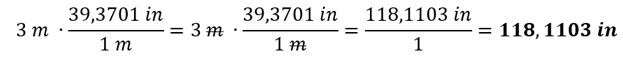
Ejemplo 2:

Convertir 2 pies (ft) a metros (m).

Solución:

Para convertir a metros, usaremos un factor de conversión, teniendo en cuenta que: 1 pie es igual a 0,3048 metros.

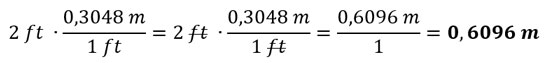
Ejemplo 3:

Convertir 4,5 millas (mi) a kilómetros (km)

Solución:

Para convertir a metros, usaremos un factor de conversión, teniendo en cuenta que: 1 milla (mi) es igual a 1,60934 kilómetros.

ACTIVIDAD EN CASA:

EJERCICIO 1. Convierta 6 km a pies

 EJERCICIO 2. Convierta 5 millas/h a m/s 

EJERCICIO 3. Convierta 96500 cm³/min a gal/s

EJERCICIO 4. Convierta 1.2 km a in "pulgadas"

ESTADIITICA:

DIAGRAMAS DE CAJAS:

DIAGRAMAS DE CAJAS Y BIGOTES

PROBLEMA DE CAJA Y BIGOTE.

En un bosque plantaron veinte (N=20) árboles y, al cabo de unos años, se mide la altura para ver su evolución. Un muy buen método para ver cómo han crecido y comprobar si existen valores extremos es el diagrama de caja. Mediante esta representación gráfica podemos ver si hay árboles que han crecido más o menos de lo habitual.

1. Se ordenan los datos
2. Se calculan los tres cuartiles.

3. 
   
   A partir del conjunto ordenado calculamos los cuartiles:

1. Los tres cuartiles son Q1=4,20, Q2=5,50 y Q3=6,42.

2. Se calculan los límites admisibles inferior y superior (LI y LS) para determinar los valores extremos.

3. 
   

4. 
   

   El rango intercuartílico es:

   
   
   

   A partir del rango calculamos los límites:

   

   
   
   
   

   
   
   

   Los valores extremos serán todos los árboles que midan menos de 0,96m o más de 9,59m. Tenemos dos árboles, uno de 0,94m y otro de 10,14m que serán valores extremos. Estos valores los representamos con puntos en el diagrama de caja.

5. El mínimo es el menor elemento del conjunto que sea mayor o igual al límite inferior. El máximo es el mayor elemento que sea menor o igual al límite superior. En este caso, el mínimo es 2,98 y el máximo 7,13.
6. Se dibujan los brazos del diagrama de caja. El brazo inferior irá desde el primer cuartil hasta el mínimo (desde el 4,20 a 2,98). El brazo superior abarcará desde el tercer cuartil hasta el máximo (desde el 6,42 hasta el 7,13).
7. Los dos puntos extremos se representan mediante un punto o círculo.

El diagrama de caja del conjunto de la altura de estos veinte árboles es:

Esta representación proporciona una visión rápida de la distribución, apreciándose una asimetría al no estar Q2 en el centro, en este caso porque hay árboles más altos que la mediana cuya altura está más separada de la mediana que los que tienen una altura inferior a ella, que están más agrupados. También se puede apreciar la existencia de valores extremos.