	ÁREA: MATEMATICA	GRADO: 10°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL 15 DE OCTUBRE DEL 2024	PERIODO: CUARTO
	VALOR: LA AMISTAD Y LA PAZ	FRASE: "SOMOS INTEGRALES ASI NOS HIZO DIOSQUERIDOS AMIGOS OFRECE ESTA OPCION EDUCACION EN SABERES,VALOR Y FORMACION BUSCANDO EN NOSOTRO SIEMPRE LO MEJOR"

FECHA: DEL 15 DE OCTUBRE DEL 2024

GRADO: 10°

TEMA: VECTORES

SUBTEMA: VECTORES EN EL PLANO

LOGRO. Realiza e interpreta las graficas de vectores.

ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿que es un vector? lluvia de ideas.

EXPLORO PAGINA 158.

VECTORES EN EL PLANO.

Vectores en el Plano

Si bien hemos podido identificar subconjuntos en el plano cartesiano con figuras geométricas tales como rectas, parábolas u otro tipo figuras determinadas por funciones, también podemos identificar en el plano otro tipo de elementos, por ejemplo, al estudiar fenómenos físicos como la aplicación de una fuerza, se debe especificar la magnitud y la dirección con que esta ha sido aplicada; para esto se definen los vectores.

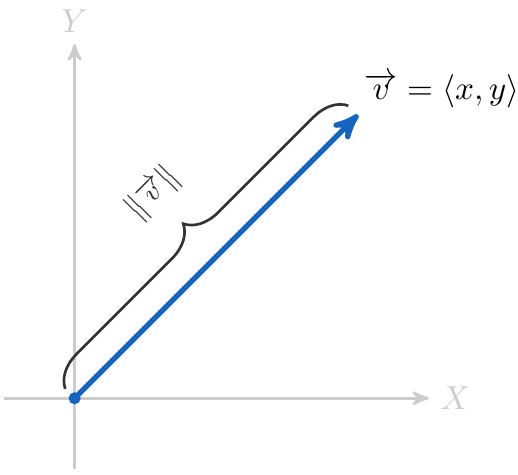
Intuitivamente, diremos que un vector es elemento que tiene una magnitud y una dirección y; geométricamente, se representa con una flecha que tiene una longitud y una inclinación respecto al Eje X. Usualmente, los vectores se presentan con un par ordenado que denota el punto en el plano cartesiano hasta donde llega el vector, partiendo desde el origen.

De esta forma, si $P = (x,y)$ es un punto en el plano, denotamos un vector que parte desde el origen y que llega hasta el punto $P$ encerrando el par ordenado con los delimitadores $\left\langle \ , \ \right\rangle$ de la siguiente forma:

$\overrightarrow{OP} = \left\langle x , y \right\rangle$

Y lo representamos gráficamente en el plano cartesiano de la siguiente forma:

Es importante señalar cual es el origen de un vector, pero cuando esto queda sobre entendido, también se pueden denotar usando letras como $\overrightarrow{v}$ ó $\overrightarrow{A}$ . Sin embargo, siempre se debe dejar clara la forma en que el vector está definido.

Magnitud de un Vector

La magnitud de un vector también es conocida como la norma del vector y se interpreta geométricamente como la longitud de la flecha que define el vector. La norma de un vector $\overrightarrow{v}$ se denota usando delimitando el vector usando una barra vertical $\left|\overrightarrow{v}\right|$ o usando la notación de distancia euclidiana con doble barra vertical $\left\lVert \overrightarrow{v}\right\rVert$ .

La norma de un vector $\overrightarrow{v} = \left\langle x , y \right\rangle$ se calcula recurriendo al Teorema de Pitágoras y es que podemos notar que cualquier vector representa la hipotenusa de un triángulo rectángulo con catetos $x$ y $y$ de la siguiente forma:

Entonces, el Teorema de Pitágoras nos indica que

$\left\lVert \overrightarrow{v} \right\rVert^2 = x^2 + y^2$

Teniendo en cuenta esta igualdad, podemos aplicar la raíz cuadrada en ambos lados de la ecuación y de esta forma, definimos una fórmula para calcular la norma de un vector de la siguiente forma:

$\left\lVert \overrightarrow{v} \right\rVert = \sqrt{x^2 + y^2}$

Veamos en los siguientes ejemplos, como aplicar esta fórmula para calcular la norma de distintos vectores.

Ejemplos

Ejemplo 1

Considerando el vector que parte desde el origen $\overrightarrow{OP} = \left\langle 3 , 4 \right\rangle$ , calcule la norma de este.

Considerando la gráfica de este vector en el plano cartesiano, tenemos que

De esta forma, podemos usar la fórmula que se ha deducido del Teorema de Pitágoras para calcular la norma de este vector.

$\left\lVert \overrightarrow{OP} \right\rVert \ = \ \sqrt{(3)^2 + (4)^2}$

$\ = \ \sqrt{9 + 16}$

$\ = \ \sqrt{25}$

$\ = \ 5$

Ejemplo 2

Considerando el vector que parte desde el origen $\overrightarrow{u} = \left\langle -2 , 2 \right\rangle$ , calcule la norma de este.

Considerando la gráfica de este vector en el plano cartesiano, tenemos que

De esta forma, podemos usar la fórmula que se ha deducido del Teorema de Pitágoras para calcular la norma de este vector.

$\left\lVert \overrightarrow{u} \right\rVert \ = \ \sqrt{(-2)^2 + (2)^2}$

$\ = \ \sqrt{4 + 4}$

$\ = \ \sqrt{8}$

Ejemplo 3

Considerando el vector que parte desde el origen $\overrightarrow{v} = \left\langle -5 , -1 \right\rangle$ , calcule la norma de este.

Considerando la gráfica de este vector en el plano cartesiano, tenemos que

De esta forma, podemos usar la fórmula que se ha deducido del Teorema de Pitágoras para calcular la norma de este vector.

$\left\lVert \overrightarrow{v} \right\rVert \ = \ \sqrt{(-5)^2 + (-1)^2}$

$\ = \ \sqrt{25 + 1}$

$\ = \ \sqrt{26}$

Ejemplo 4

Considerando el vector que parte desde el origen $\overrightarrow{A} = \left\langle 4 , -2 \right\rangle$ , calcule la norma de este.

Considerando la gráfica de este vector en el plano cartesiano, tenemos que

De esta forma, podemos usar la fórmula que se ha deducido del Teorema de Pitágoras para calcular la norma de este vector.

$\left\lVert \overrightarrow{A} \right\rVert \ = \ \sqrt{(4)^2 + (-2)^2}$

$\ = \ \sqrt{16 + 4}$

$\ = \ \sqrt{20}$

Dirección de un Vector

La dirección de un vector también es conocida como el sentido del vector y se interpreta geométricamente como el ángulo (menor de 180 grados) que forma la flecha que define el vector con la parte positiva del Eje X.
La dirección un vector $\overrightarrow{v} = \left\langle x , y \right\rangle$ se calcula recurriendo a la trigonometría, pues podemos notar que cualquier vector representa la hipotenusa de un triángulo rectángulo con catetos $x$ y $y$ , considerando el siguiente gráfico
Podemos definir las siguientes expresiones trigonométricas.
$\sin(\alpha) = \dfrac{y}{\left\lVert \overrightarrow{v} \right\rVert}$
$\cos(\alpha) = \dfrac{x}{\left\lVert \overrightarrow{v} \right\rVert}$
$\tan(\alpha) = \frac{y}{x}$
Teniendo en cuenta estas igualdades, podemos aplicar las función inversa correspondiente a cada función trigonométrica y así, definimos una fórmula para calcular el ángulo del vector $\overrightarrow{v}$ respecto al Eje X, usando cualquiera de las siguientes igualdades:
$\alpha = \arcsin\left( \dfrac{y}{\left\lVert \overrightarrow{v} \right\rVert} \right)$
$\alpha = \arccos\left( \dfrac{x}{\left\lVert \overrightarrow{v} \right\rVert} \right)$
$\alpha = \arctan \left( \dfrac{y}{x} \right)$
De forma general, se usa la fórmula que involucra el arco coseno, pues es la que determina el ángulo formado entre el vector y el Eje positivo de X directamente.
Veamos en los siguientes ejemplos, como aplicar esta fórmula para calcular la dirección de distintos vectores.

Ejemplos

Ejemplo 5

Considerando el vector que parte desde el origen $\overrightarrow{OP} = \left\langle 3 , 4 \right\rangle$ , calcule la dirección de este.
Considerando la gráfica de este vector en el plano cartesiano, tenemos que
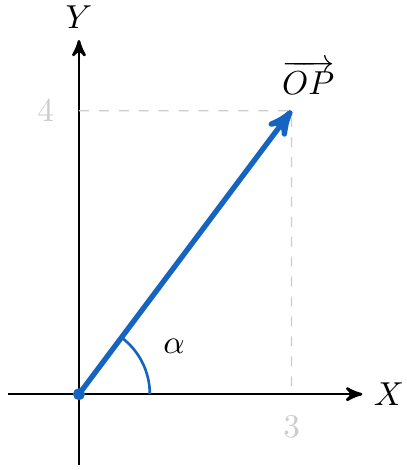
De esta forma, podemos usar cualquiera de las fórmulas que se han deducido de las funciones trigonométricas para calcular la dirección de este vector, pero primero debemos calcular la norma del vector
$\left\lVert \overrightarrow{OP} \right\rVert \ = \ \sqrt{(3)^2 + (4)^2}$

$\ = \ \sqrt{9 + 16}$

$\ = \ \sqrt{25}$

$\ = \ 5$
Entonces, conociendo la norma del vector, podemos usar la fórmula que involucra el coseno
$\alpha \ = \ \arccos\left( \dfrac{y}{\left\lVert \overrightarrow{OP} \right\rVert} \right)$

$\ = \ \arccos \left( \frac{3}{5} \right)$

$\ \approx \ 53.13^{\circ}$

Ejemplo 6

Considerando el vector que parte desde el origen $\overrightarrow{u} = \left\langle -2 , 2 \right\rangle$ , calcule la dirección de este.
Considerando la gráfica de este vector en el plano cartesiano, tenemos que
De esta forma, podemos usar cualquiera de las fórmulas que se han deducido de las funciones trigonométricas para calcular la dirección de este vector, pero primero debemos calcular la norma del vector
$\left\lVert \overrightarrow{u} \right\rVert \ = \ \sqrt{(-2)^2 + (2)^2}$

$\ = \ \sqrt{4 + 4}$

$\ = \ \sqrt{8}$
Entonces, conociendo la norma del vector, podemos usar la fórmula que involucra el coseno
$\alpha \ = \ \arccos\left( \dfrac{y}{\left\lVert \overrightarrow{u} \right\rVert} \right)$

$\ = \ \arccos \left( \frac{-2}{\sqrt{8}} \right)$

$\ = \ 135^{\circ}$

Ejemplo 7

Considerando el vector que parte desde el origen $\overrightarrow{v} = \left\langle -5 , -1 \right\rangle$ , calcule la dirección de este.
Considerando la gráfica de este vector en el plano cartesiano, tenemos que
De esta forma, podemos usar cualquiera de las fórmulas que se han deducido de las funciones trigonométricas para calcular la dirección de este vector, pero primero debemos calcular la norma del vector
$\left\lVert \overrightarrow{v} \right\rVert \ = \ \sqrt{(-5)^2 + (-1)^2}$

$\ = \ \sqrt{25 + 1}$

$\ = \ \sqrt{26}$
Entonces, conociendo la norma del vector, podemos usar la fórmula que involucra el coseno
$\alpha \ = \ \arccos\left( \dfrac{y}{\left\lVert \overrightarrow{v} \right\rVert} \right)$

$\ = \ \arccos \left( \frac{-5}{\sqrt{26}} \right)$

$\ \approx \ 168.69^{\circ}$

Ejemplo 8

Considerando el vector que parte desde el origen $\overrightarrow{A} = \left\langle 4 , -2 \right\rangle$ , calcule la dirección de este.
Considerando la gráfica de este vector en el plano cartesiano, tenemos que
De esta forma, podemos usar cualquiera de las fórmulas que se han deducido de las funciones trigonométricas para calcular la dirección de este vector, pero primero debemos calcular la norma del vector
$\left\lVert \overrightarrow{A} \right\rVert \ = \ \sqrt{(4)^2 + (-2)^2}$

$\ = \ \sqrt{16 + 4}$

$\ = \ \sqrt{20}$
Entonces, conociendo la norma del vector, podemos usar la fórmula que involucra el coseno
$\alpha \ = \ \arccos\left( \dfrac{y}{\left\lVert \overrightarrow{A} \right\rVert} \right)$

$\ = \ \arccos \left( \frac{4}{\sqrt{20}} \right)$

$\ \approx \ 26.56^{\circ}$

Ciencias Exactas

PRINCIPAL

BIENVENIDA

martes, 1 de octubre de 2024

CLASE DE MATEMATICA GRADO 10° DEL 15 DE OCTUBRE DEL 2024 SEMANA # 33 TEMA: VECTORES

Vectores en el Plano

Magnitud de un Vector

Ejemplos

Ejemplo 1

Ejemplo 2

Ejemplo 3

Ejemplo 4

Dirección de un Vector

Ejemplos

Ejemplo 5

Ejemplo 6

Ejemplo 7

Ejemplo 8

No hay comentarios.:

Publicar un comentario