Ciencias Exactas: CLASE DE MATEMATICA GRADO 10° DEL 24 DE OCTUBRE DEL 2024 TEMA: MATRICES

	ÁREA: MATEMATICA	GRADO: 10°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL 24 DE OCTUBRE DEL 2024	PERIODO: CUARTO
	VALOR: AMISTAD	FRASE: "SOMOS INTEGRALES ASI NOS HIZO DIOSQUERIDOS AMIGOS OFRECE ESTA OPCION EDUCACION EN SABERES,VALOR Y FORMACION BUSCANDO EN NOSOTRO SIEMPRE LO MEJOR"

FECHA: DEL 24 DE OCTUBRE DEL 2024

GRADO: 10°

TEMA: MATRICES

SUBTEMA: MATRICES

LOGRO. Define una matriz, su utilidad y aplicación en otros campos del saber.

ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿que es una matriz? lluvia de ideas.

EXPLORO PAGINA 194.

MATRICES.

Concepto de matriz

Se denomina matriz a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas. Este sería un ejemplo de una matriz " $\text{[math]}$ "

$\text{[math]}$

Cada uno de los números de que consta la matriz se denomina elemento. Así, los elementos de nuestra matriz del ejemplo anterior serían lo números que contiene $\text{[math]}$ .

El número de filas y columnas de una matriz se denomina dimensión de una matriz.

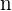Una matriz $\text{[math]}$ de $\text{[math]}$ filas y $\text{[math]}$ columnas podemos denotarla como $\text{[math]}$ (siempre el número de la izquierda en el subíndice indica las filas, mientras que el de la derecha las columnas) o $\text{[math]}$ (está entre paréntesis), y un elemento cualquiera de la misma, que se encuentra en la fila $\text{[math]}$ y en la columna $\text{[math]}$ , por $\text{[math]}$ (no lleva paréntesis). Un elemento se distingue de otro por la posición que ocupa, es decir, la fila y la columna a la que pertenece.

$\text{[math]}$

Ejemplo:

Del ejemplo anterior, para nuestra matriz $\text{[math]}$

$\text{[math]}$

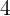tendríamos que sus elementos, al distinguirlos por posición, serían $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ y $\text{[math]}$ . Además, su dimensión es de $\text{[math]}$ filas y $\text{[math]}$ columnas, por lo tanto podemos denotar a $\text{[math]}$ como $\text{[math]}$ o $\text{[math]}$ .

Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan el mismo lugar en ambas, son iguales. En forma matemática, si tenemos las matrices $\text{[math]}$ y $\text{[math]}$

$\text{[math]}$

Entonces $\text{[math]}$ y $\text{[math]}$ son iguales si $\text{[math]}$ , $\text{[math]}$ y $\text{[math]}$ para cualquier $\text{[math]}$ y $\text{[math]}$ .

Ejemplo

Dadas las matrices

$\text{[math]}$

Tenemos que $\text{[math]}$ y $\text{[math]}$ son iguales ya que tienen la misma dimensión y los elementos de las mismas posiciones también son iguales. Sin embargo, $\text{[math]}$ y $\text{[math]}$ no son iguales ya que $\text{[math]}$ , pero $\text{[math]}$ , por lo tanto $\text{[math]}$ .